(1)Dr. Scott A. Sarra , October 17, 2002
Method of Characteristics Applet
audience: Undergraduate students in a partial differential equations class, undergraduate (or graduate) students in mathematics or other sciences desiring a brief and graphical introduction to the solutions of nonlinear hyperbolic conservation laws or to the method of characteristics for first order hyperbolic partial differential equations.
abstract: This web article and accompanying applet introduces the method of characteristics for solving first order partial differential equations (PDEs). First, the method of characteristics is used to solve first order linear PDEs. Next, the method of characteristics is applied to a first order nonlinear problem, an example of a conservation law. It is discussed why the method may breakdown for nonlinear problems. Difficulties that appear in the nonlinear case, but are absent in the linear case, are examined and the mathematical resolutions of these problems are introduced. Concepts dealing with the solutions of nonlinear hyperbolic conservation laws are introduced and explored graphically. However, the detailed explanation of such concepts may take up entire text books, and the concepts are not explored in detail or with rigor in this short paper. References to more detailed material is given.
* This article and applet appear in the Journal of Online Mathematics and its Applications (JOMA), Volume 3, February 2003.
The method of characteristics is a method which can be used to solve the initial value problem (IVP) for general first order (only contain first order partial derivatives) PDEs. Consider the first order linear PDE
in two variables along with the initial condition
. The goal of the method of characteristics, when applied to
this equation, is to change coordinates from (x,t) to a new coordinate system
in which
the PDE becomes an ordinary differential equation (ODE) along certain curves in
the x-t plane. Such curves,
, along which the solution of the PDE reduces to an
ODE, are called the characteristic curves or just the characteristics.
The new variable s will vary, and the new variable
will be
constant along the characteristics. The variable will change along the initial
curve in the x-t plane (along the line t=0). How do we find the characteristic
curves? Notice that if we choose
(2a) and
(2b) then we have
and along the characteristic curves, the PDE becomes the ODE
. (3)
Equations (2a) and (2b) will be referred to as the characteristic equations.
The general strategy for applying the method of characteristics to a PDE of
the form (1) is: (step 1) Solve the two
characteristic equations, (2a) and (2b). Find the constants of integration by setting
(these will be points along the t=0 axis in the x-t plane) and t(0)=0. We now
have the transformation from
to
,
and
.
(step 2) Solve the ODE (3) with initial condition
, where
are the
initial points on the characteristic curves along the t=0 axis in the x-t
plane. (step 3) We now have a solution
. Solve
for s and
in terms of x and t (using the results of step 1) and substitute these values
in to
get the solution to the original PDE as
.
We will examine the method of characteristics for three different PDEs: the
constant coefficient advection equation, the variable coefficient advection
equation, and inviscid Burgers' equation. For all three examples, the initial
conditions are specified as
. The
examples take a slightly simpler form than the general equation (1). All three examples have b(x,t)=1 and c(x,t)=0. In this case
characteristic equation (2b) becomes
. The solution is t=s + k.
Using the initial condition t(0)=0, we determine that the constant is k=0, and
we have that s=t. In this special case with b(x,t)=1, we only have one
characteristic equation to solve. Before proceeding to the examples, let us
restate the general strategy in terms of this special case that we are
considering in the examples.
(step1) Solve the characteristic equation (2a),
, with the initial condition
.
(step 2) Solve the ODE (3), which in this case
simplifies to
, with
initial condition
(step
3) We now have a solution
. Solve
for in
terms of x and t (using the results of step 1) and substitute for
in
to get
the solution to the original PDE as
.
Our first example, the advection equation, is the PDE
(4) where a is a real constant. The constant a is referred
to as the wave speed or velocity of propagation. This is the rate
at which the solution will propagate along the characteristics. The velocity is
constant, so all points on the solution profile will move at the same speed a.
Now we apply the method of characteristics outlined in the 3 steps in the
previous section. (step 1) The characteristic equation (2a) to solve is
with
the initial condition
.
The solution gives the characteristic curves,
where
is the
point where each curve intersects the x-axis in the x-t plane. (step
2) Solve equation (3),
with
initial condition
. The
solution is
.
(step 3). The characteristic curves are determined by,
, so
, and
the solution of the PDE is
.
To verify that
does
indeed remain constant along the characteristics, we differentiate
along one
of these curves to find the rate of change of u along the characteristic:
So we find that the rate of change is zero, verifying that u is constant along the curve.
By writing the characteristic curves as
it is easy to see that in the x-t plane, the characteristics are parallel lines
with slope 1/a. The slope of the characteristics depends only on the constant
a. Experiment in the applet with different values (a is changed through the
dialog box which is displayed when the parameters button is pressed) of the
wave speed, a. Set
to observe
the solution profile moving in the opposite direction and observe the negative
slope of the characteristics.
The variable coefficient advection equation is
(5) where for this example we have taken
. The wave
speed depends on the spatial coordinate, x. Thus, the speed of a point on the
solution profile will depend on the horizontal coordinate, x, of the point.
(step 1) The characteristic equation (2a) to
solve is
with
the initial condition
.
Solving it gives the characteristic curves
.
(step 2) Solve equation (3),
with
initial condition
. The
solution is
.
(step 3) The characteristic curves are determined by
, so
and the solution of the PDE in the original variables is
.
View the variable coefficient advection equation simulation in the applet. Notice that the characteristics are not straight lines. Also observe that the characteristics do not intersect.
A very important class of partial differential equations is that of conservations laws. As their name indicates, they include those equations that model the conservation laws of physics: mass, momentum, energy, etc. A scalar conservation law in one space dimension takes the form
where F(u) is a flux function. In general, conservation laws are nonlinear.
For a derivation of the conservation law (6), the interested
reader may consult [2, p. 31] or [3 p.
75]. We will use the method of characteristics to examine a one dimensional
scalar conservation law, inviscid Burgers' equation, which takes the form of a
nonlinear first order PDE. Inviscid Burgers' equation will have
.
The inviscid Burgers' equation is
or
equivalently
. The
wave speed depends on the solution,
. Thus, the
speed of a point on the solution profile will depend on the vertical
coordinate, u, of the point. Inviscid Burgers' equation is not of the form of
the linear first order PDE (1), as it is nonlinear, so our
earlier analysis do not apply directly. However, from our experience with the
constant (4) and variable coefficient (5)
advection equations, we are led to set the characteristic equation to be
. If
x(t) is a solution of this equation, then u[x(t),t] is the restriction of u to
this curve. Also, along this curve,
Thus, this solution u[x(t),t] will not change with time along the curve, so
it is a characteristic curve. If we know the initial condition
, we can
find the characteristic curve by substituting this value into the
characteristic equation
.
The right hand side of the equation is constant, indicating that the
characteristic curves will be straight lines, as in the constant coefficient
advection equation case. The characteristic curve will be
. The solution of the initial value problem can be written as
.
The solution is given implicitly and in all but the simplest cases, it will be
impossible to determine the solution explicitly. The characteristics are
straight lines, but the lines do not all have the same slope. It will be
possible for the characteristics to intersect. If we write the characteristics
as
, we see that in the x-t plane that they are lines with slope
.
The slope of the characteristics depends on the point
and on the
initial data.
Unlike the first two examples, it is possible for the characteristics to intersect. If the initial data is smooth, then the method of characteristics can be used to determine the solution for small enough t such that the characteristics do not intersect. For larger t, after characteristics have interested, the PDE will fail to have a classical solution (a classical solution is a single valued solution or a function), as the information obtained by following the characteristics will produce a multivalued solution, or possibly, no solution at all. To overcome this lack of existence of a classical solution, we must introduce a broader notion of a solution, a weak solution. Roughly speaking, a weak solution may contain discontinuities, may not be differentiable, and will require less smoothness to be considered a solution than a classical solution. Working with the weak solution of a PDE usually requires that the PDE be reformulated in an integral form. If a classical solution to the problem exists, it will also satisfy the definition of a weak solution.
If the characteristics on both sides of a discontinuity of a piecewise
continuous weak solution impinge on the discontinuity curve in the direction of
increasing t, the weak solution is called a shock.
For inviscid Burgers' equation, the time at which the characteristics cross and
a shock forms, the "breaking" time, can be determined exactly
as, 
[1, p. 25]. The formula can be used if the
equation has smooth initial data (so that it is differentiable). From the
formula for 
, we can see that the solution will break and a shock will form if
is
negative at some point. The discontinuous weak solution, in this case a
shock wave, will travel at a speed given by the Rankine-Hugoniot
condition. (see [1, p. 31] and [2,
p. 46]). For inviscid Burgers' equation the shock
speed, s, is given by
where
is the value
of u on the left side of a discontinuity and
is the
value of u on the right side of the discontinuity. In addition to
characteristics crossing and a shock forming, another possible way the method
of characteristics can break down, and a discontinuity can form, is if the
characteristics on both sides of the discontinuity emanate from it, rather than
go into it. Then the discontinuity is called a rarefaction
wave. (see applet simulation and rarefaction example below)
By expanding our class of solutions to include weak solutions, we no longer
have uniqueness of the solution of the initial value problem. Additional
criteria must be used to pick out the physically correct weak solution. The
selection criteria for physically meaningful discontinuous weak solutions is
called an entropy condition. A different method to pick out the
physically correct weak solution, but one that picks of the same physically
correct weak solution as the entropy condition does, is a vanishing
viscosity approach. For inviscid Burgers' equation, this would amount to
finding solutions to Burgers' equation,
, in
the limit as
. A
graphical technique for constructing weak solutions for problems with shocks is
the equal area rule ([4, p. 42] and [1, p. 34]). The application of the equal area rule starts with
the multivalued solution constructed by using the method of characteristics and
then eliminates the multivalued parts by inserting shocks in a way that
eliminates the multivalued solution but keeps the area under the curve the
same. The equal area rule is a result of conservation. The integral of the
discontinuous weak solution must be the same as the integral of the multivalued
solution.
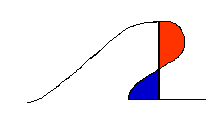
The red area is subtracted from the multivalued solution and the blue area is added. The sum of the blue and unshaded areas then makes up the weak solution. In the applet, observe in the shock problems for inviscid Burgers' equation how the plotted weak solutions appear to be applying this equal area rule to the multivalued solutions produced by the method of characteristics.
For inviscid Burgers' equation with piecewise constant initial data, we are
able to find a formula for the weak solution. For more complicated initial data
this will most likely not be the case. Asymptotic formulas (accurate in the
limit as
, see
reference [4]) for the weak solutions to the problems may
exist, but are of little use computationally. Thus, numerical methods that are
capable of producing good approximations to the exact entropy satisfying weak
solution are important. In general, numerical methods for nonlinear hyperbolic
conservation laws are more complicated and difficult to develop than numerical
methods for elliptic and parabolic PDEs. For the inviscid Burgers' problem with
the sine wave, N-wave, and single hump initial data, the applet uses a
numerical method to approximate the exact entropy satisfying weak solution. The
method in a second order nonoscillatory finite difference method called
Roe's method which employs the used of a flux limiter (the Superbee
limiter is used) to suppress numerical oscillations. When using the simulations
in the applet that calculate the weak solutions by the numerical method, the
ratio 
must be kept below a certain threshold, or the method will become
unstable and the numerical approximation will blow up. The interested reader
should consult references [1] and [3]
for details.
The following initial conditions for inviscid Burgers' equation are coded in the applet. The first two problems are Riemann problems, i.e., they have piecewise constant initial data consisting of one discontinuity.
This problem has an initial condition
. The
characteristics intersect and a shock forms immediately for t>0. The exact
entropy satisfy weak solution is
where the shock speed is given by
.
The exact weak solution is plotted in the applet. This problem is discussed in
detail in references [1 p. 28], and [3,
p. 82].
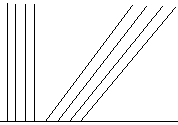
The initial condition
produces characteristics (see image below and the applet also) such
that there is no characteristic information available in some regions of the
x-t plane.
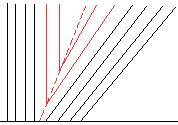
A entropy violating weak solution is
, where s is the same as the Riemann shock problem above. This
solution corresponds to filling in the missing characteristic information as
shown in red below.
For this problem, it can be shown that infinitely many weak solution exists [1, p. 30].
A entropy satisfying weak solution is
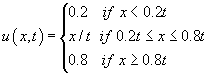. This solution corresponds to filling in the missing characteristic
information as shown in red in the image below.
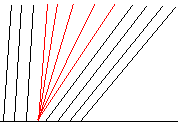
This problem is discussed in detail in references [1 p. 28], and [3, p. 82].
The initial condition is
. Notice
that
has
a minimum value of
. Thus,
the breaking time will be
(approximately t=0.16) . This problem is discussed in detail in
reference [3, p. 77]. The weak solution is computed by
using Roe's method.
The initial condition is
. The
solution consists of both a left and right moving shock. The weak solution is
computed by using Roe's method. This problem is discussed in detail in
reference [4, p. 48] and in [1, p. 32]
The initial condition is
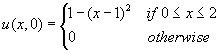. The
solutions consist of one right moving shock. The weak solution is computed by
using Roe's method. This problem is discussed in detail in reference [4, p. 46]
Use of the applet require the Java 1.4 browser plug-in. If you do not have it installed on your computer, the script on the web page should direct you to the site where you can freely get the plug-in and install it. If you do not have the plug-in, and the script does not direct you to the plug-in, follow this link.
The applet provides two views. The window on the left shows the initial condition advancing in time, while the window on the right shows the data advancing along the characteristics in the x-t plane.
Select one of the three example from the equations menu: the advection equation, the variable coefficient advection equation, or inviscid Burgers' equation. The inviscid Burgers' equation option has five submenus corresponding to five different initial conditions. Press the go button to start the animation, the stop button to stop the animation, and the reset button to return to the initial conditions. For inviscid Burgers' equation, the applet can plot the weak solution (as a solid black curve) to the problem. This option may be turned on by checking it on the options menu.
Pressing the parameters button pops up a dialog which allows five parameters to be changed by the user:
